Three-Phase Diagram of Soil & Volumetric Relations

Soil is a combination of grains, water, and air, hence forming a three-phase material. But when the soil is dry (no water) and saturated (no air), there will only be two phases, making it a two-phase material.

Arrangement of Soil Grains 

 
Now, the relative proportions of these three phases play an important role in the engineering behavior of the soil. These properties are used in geotechnical problems like earthworks, and laboratory tests to compute weights and volumes of the three phases.

Let's discuss the three-phase diagram of soil and important phase relationships used in geotechnical engineering calculations.

Three-Phase Diagram of Soil

Soil is a three-phase material composed of air (a), water (w), and soil grains or solids (s) [Fig.2.]. Let’s represent soil as a phase diagram combining all similar phases as shown in Figure.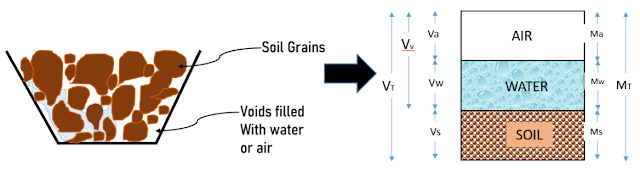

Three-Phase Diagram of Soil

As shown in the figure, the corresponding mass or weight of the material is ‘M’, and the volume is ‘V’, represented in the right and left respectively.

The final figure represents the three-phase diagram of soil. The volume of air, water, and soil are Va, Vw, and Vs, while the mass is Ma, Mw, and Ms respectively. Here, we know that the mass of air Ma = 0.

The Total Volume is the sum of the total volume of air, water, and soil grains. that gives,

V_T = Va + Vw + Vs; 

and the total mass is the sum of the mass of air, water, and soil grains.

 M_T = Ma + Mw + Ms;

Total Volume of Voids is given as Vv, which is the sum of the volume of air and volume of water. This means the voids can be filled either by air or water. 

Vv = Va + Vw

Let's find the relations for certain properties of the soil, based on the three-phase diagram.

1. Void Ratio (e)

The void ratio is the ratio of void volume (Vv) ratio to the soil grain volume (Vs). This gives

e = Vv/Vs

Void ratio gives a measure of the volume of voids present in the soil mass. The higher the void ratio, the higher the presence of voids, and the higher the permeability of the soil. Such soils need to be compacted before use, especially for the construction of foundations. Or else, under the action of load, the soil will undergo large deformations. 

2. Porosity (n)

The porosity of soil is defined as the ratio of void volume (Vv) to the total volume (Vt). This property is expressed in percentage.

e = Vv/Vt

The porosity varies greatly from one kind of soil to another. The amount of porosity depends on the minerals that make up the soil and the structural arrangement of the soil grains. 

Void ratio and porosity are inter-related  and given the formula:

e = n / (n-1);

3. Degree of Saturation (S)

The degree of saturation is defined as the ratio of the water volume (Vw) to the void volume (Vv). It is expressed in percentage.

S = Vw/Vv

The degree of saturation indicates how extent the empty space of the soil is filled with water. When the soil is completely dry, S=0; when the soil is fully saturated, S= 100%. 

4. Air Content (a)

Air content is defined as the ratio of air volume (Va) to the volume of the voids. It is given by,

a = Va/Vv;

5. Percentage Air Voids (na)

The percentage of air voids is given as the ratio of the volume of air (Va) to the total volume (V). It is expressed in percentage.

na= Va/V; 

When the soil is fully saturated, the percentage of air voids is equal to zero

5 Volumetric Relationships in Soil Engineering

1. Relationship Between Porosity (n) and Void Ratio (e)

Porosity is given by:

n = Vv/V

1/n = V/Vv

V = Vv + Vs

Hence we have,

1/n = (Vv +Vs)Vv = 1+ (Vs/Vv) = 1 + (1/e) = (1+e)/e

Hence,

n = e /(1+e)

2. Relationship Between Percentage Air Voids (na) and Air Content (a)

We know that, the percentage of air voids 

na  = Va/V

The above relation can be written as follows by 

na = (Va/Vv) x (Vv/V)  

na = n x ac

Where, na=porosity; a is the air content